We consider the problem of finding and classifying Einstein metrics on spheres that are invariant under certain rotational symmetries. In the blog post below, we briefly introduce the research and compare our result with a famous paper from Christoph Bӧhm.
We call a manifold a space that locally looks like dimensional real space. For example, the surface of the earth looks, to an observer, like a flat plane. Thus, an example of a -dimensional manifold is a sphere, denoted . Extrapolating, we find that , the set of points of distance from the origin in dimensional real space, is an -dimensional manifold.
However, when we define a manifold formally, we are only able to give a topology, with some notion of smoothness and what smooth functions look like. That means that if we deform our manifold, we don’t really change it. For example, if we imagine deflating the sphere like we would a soccer ball, we still have a manifold with the same overall topological structure. This becomes a problem if we want to analyse the geometry of a manifold. To rigorously develop geometry, we need to define a metric , allowing us to define lengths and angles of tangent vectors, providing all the information we need.
Curvature is one way we can measure the geometry of a manifold. One important measure of curvature is the Ricci curvature, which describes the local behaviour of volume on the manifold. We can use the Ricci curvature to define an Einstein manifold, which for our purposes simply means it has a “nice” shape. These manifolds satisfy the equation for some real constant .
Over the summer I was tasked to find all the possible “nice” geometries of an dimensional sphere that are symmetric under particular rotations. Specifically, I wanted to show an Einstein manifold which can be moulded into a dimensional sphere, that looks the same when rotated in its first or last coordinates must be round.
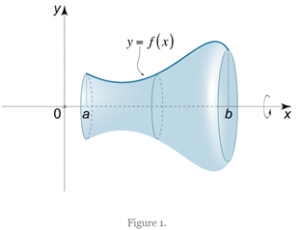
First, we consider a simpler example. Let be a -dimensional real smooth function defined from to , where it is at its endpoints, that is . Then, similar to figure 1, if we rotate this function about the axis then it is deformable into a sphere and is rotationally symmetric about the axis. In my project this was then rotated again in higher dimensions to achieve the desired symmetries. Then, we investigated smoothness conditions on the boundaries and the Einstein condition above to eventually conclude that what we described must be round.
Figure 1 [2]
One would expect, given enough symmetries via rotations, such as in the case I investigated, then the sphere would need to always be round. However, if we instead want chose invariance under slightly different rotations such as in the first or last coordinates then the shape might not necessarily
be round. In fact, Christoph Bӧhm was able to construct an infinite amount of non-round Einstein spheres in dimensions to [1].
[1] Bӧhm, C 1998, `Inhomogeneous Einstein metrics on low-dimensional spheres other low-dimensional spaces’, Inventiones Mathematicae, vol. 134, no. 1, pp. 145-176.
Patrick Donovan
The University of Queensland