Mathematicians have been interested in the study of shapes since its very inception. In modern times, many very sophisticated tools are at the mathematicians’ disposal to study shapes. We give a simple example to motivate how one might quantify the twistedness of a shape, even in higher dimensions when it cannot be visualised.
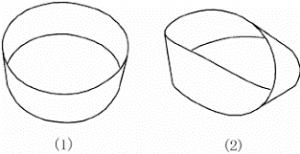
In my project I studied mathematical objects known as vector bundles. A simple example of a vector bundle is the surface of a cylinder. A cylinder can be constructed by taking a piece of paper and gluing the two ends together, as shown in Figure 1 (1).
Image courtesy of Nishiyama, Y. (2012). Playing with Mӧbius Strips. International Journal of Pure and Applied Mathematics. 78. 1121-1130.
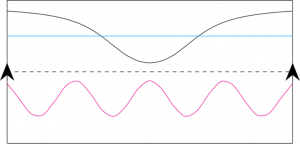
Now imagine I draw a straight line horizontally through the middle of the piece of paper, dividing it into two regions. I pose the following challenge: can you draw a curve from the left end of the paper to the right end (without your pen leaving the paper) so that
- You stay in only the top half or bottom half the entire time
- When you glue the edges of the paper together, the endpoints of your curve line up.
Hopefully your answer was yes. Several solutions are shown in Figure 2 in black, blue and red.
Now let’s look at another example of a vector bundle, called the Mӧbius band. The Mӧbius band can also be constructed by gluing together a sheet of paper. Just like the cylinder, we want to glue the ends of the paper together but this time we first turn one end by 180°, and then glue the ends together. You should end up with a shape like Figure 1 (2).
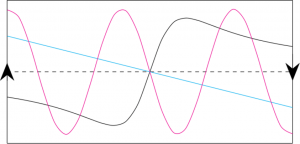
Let’s play the same game as we did before. Divide your piece of paper into two regions with a straight line. Can you draw a curve from one end of the paper to the other which satisfies the rules above? It might be helpful to imagine your piece of paper is transparent so that you can see the curve on both sides of the paper.
If you play around with this for a while (and I suggest you do!) you will find that there is no way to satisfy both of the rules. To line up the endpoints you must pass through the middle line, as shown in Figure 3.
The reason we can never succeed in this challenge now is because the Mӧbius band is twisted. In fancy maths lingo, we say the Mӧbius band is a nontrivial vector bundle. In my summer research project, I studied ways we can precisely quantify how twisted a vector bundle is, even if the vector bundles lives in higher dimensions that we cannot visualise. To attack this problem, I used many different tools from geometry, topology and calculus.
Jamie Bell
University of Wollongong