In this AMSI project, the solution I found was simply to avoid implementing the search completely. Instead, code was written to reduce (or translate) the original search problem into a problem that already had well known solutions, which I could then make use of.
Reductions are translations from one problem to another, and are often seen in computer science to show that certain problems are “hard” to solve with a computer. The idea is that if can show that a new problem can be translated into a problem that we already know is difficult, then this new problem must be at least similarly difficult to solve too.
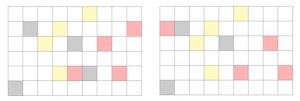
The search problem was essentially about finding a way to fit coloured puzzle pieces together perfectly without overlap, but our puzzle has the annoying rule that pieces of the same colour are linked together so that if you move one of them, the rest must move the same way (pay attention to how all the red pieces move right, then down):
The ends of the puzzle board are connected, so that pieces that are moved off the end jump to the other end of the board like shown below:
You’ll notice that if we start with a large board with lots of puzzle pieces and want to fill it completely, we end up with many possible ways to fit the pieces together. This can make the computer search time consuming
One way of doing this is to create a graph (the kind that consists of dots or vertices, with lines or edges connecting them), that can be used to show what combinations of puzzle-piece positions might fit together.
We associate every possible position for each colour of puzzle piece with a coloured vertex, and connect any two different coloured vertices that correspond to pieces that don’t overlap. Then we just need to choose one vertex of each colour, so that any two selected vertices are always connected by an edge (otherwise we would get overlapping pieces in our puzzle). This problem turns out to be the same as the “clique problem”, which is a well-known problem in computer science.
Although this reduction doesn’t really simplify the steps involved in our search, it does make the code writing far easier. Now instead of keeping track of groups of coloured puzzle pieces, we can just deal with a big collection of connected single vertices. More importantly, by translating our original problem into one which has already been solved before, we get most of the code we need for free!
So the relatively conceptual reductions that we may see in theoretical applications to transform one obscure problem to another, may be more relevant to the everyday than they seem*.
*Or, if you’re not a fan of unusual puzzles, will at least let you be occasionally lazier when programming.
Tiana Tsang Ung
UNSW